Reinforcement Learning Day 4 (Finite Markov Decision Processes’s Coursera Video Notes)
- Specifying Policies
- Value Functions
- Action-value function
- Bellman Equation Derivation
- Intuition - Bellman Eqaution
- Optimal Policy
- Summary
Specifying Policies
- Policies can only depend on current state not on previous state or time.
Value Functions
- value functions and state-action functions.
value functions regularize all the maximum return it can get (as below).
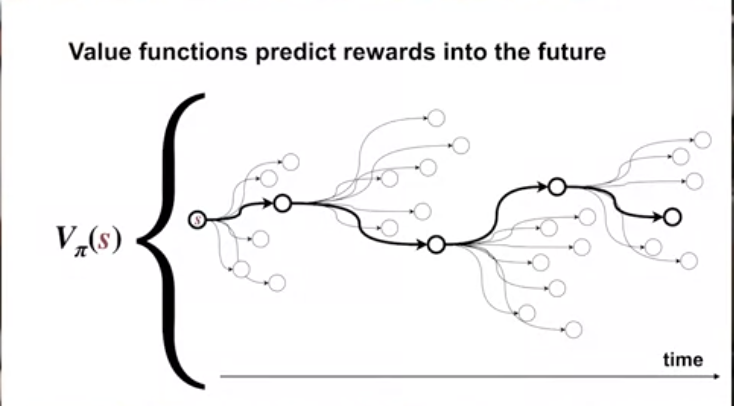
state-value function indicate the maximum reward that a state can get.
state-action $q_\pi$ functions regularize if we choose a action and keeping using $\pi$ in following states, the maximum return we can get.
Action-value function
Like value function, We call $q_{\pi}(s,a) = E_{\pi}[G_t | S_t =s, A_t = a]$ the action-value function for policy $\pi$.
Bellman Equation Derivation
First recall the return of a state is discount value * return’s sum at the beginning of a state.
the policy choose some action probability * the state action transfer probability (reward) * (reward + gamma*(future reward))

in the same way, we can infer action value function

Intuition - Bellman Eqaution
Because, when we want to calculate the expected value of the state and action, it will depend on next state… It’s infinite.
But if we use bellman-equation, it’s a equation and we can solve it!
when the equations are in huge number, there is another solution.
Optimal Policy
Optimal Policy can reach the maximum value for each state across all policy
and in the above bellman eqaution, we times a policy probability that choose an action in a state. But for the Optimal policy is fixed. We will choose the optimal action. Thus, we will rewrite it as max a

the optimal policy cannot be solved in a linear system.
optimal value function means we can choose the maximum + reward for the next state; thus, we can fixed the optimal actions.
Summary
A policy depends only on the current state.
but it is an ideal that reinforcement learning agents can only approximate to varying degrees. In reinforcement learning we are very much concerned with cases in which optimal solutions cannot be found but must be approximated in some way.